Image by Freepik

Completing the Square, one of the important and easiest methods to solve a quadratic equation of the form ax² + bx + c. It is an application of the famous algebraic formula (a + b)². Please check out my previous **article to understand the visual explanation for *(a + b)²*

Why quadratic equations are that difficult to solve?🤔 Because x appears twice in the equation. Is that worse? Let us consider an example equation x2 + 2x + 1= 0 and rearrange it to make x appear once.

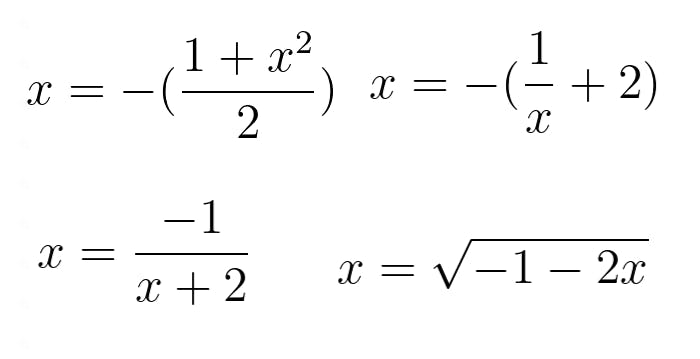
How hard we try, we end up having 2 x’s in our equation.

Completing the Square 💁

Here comes our friend. Let us rearrange our equation a bit x² + 2x = -1 and visualize in the form of shapes

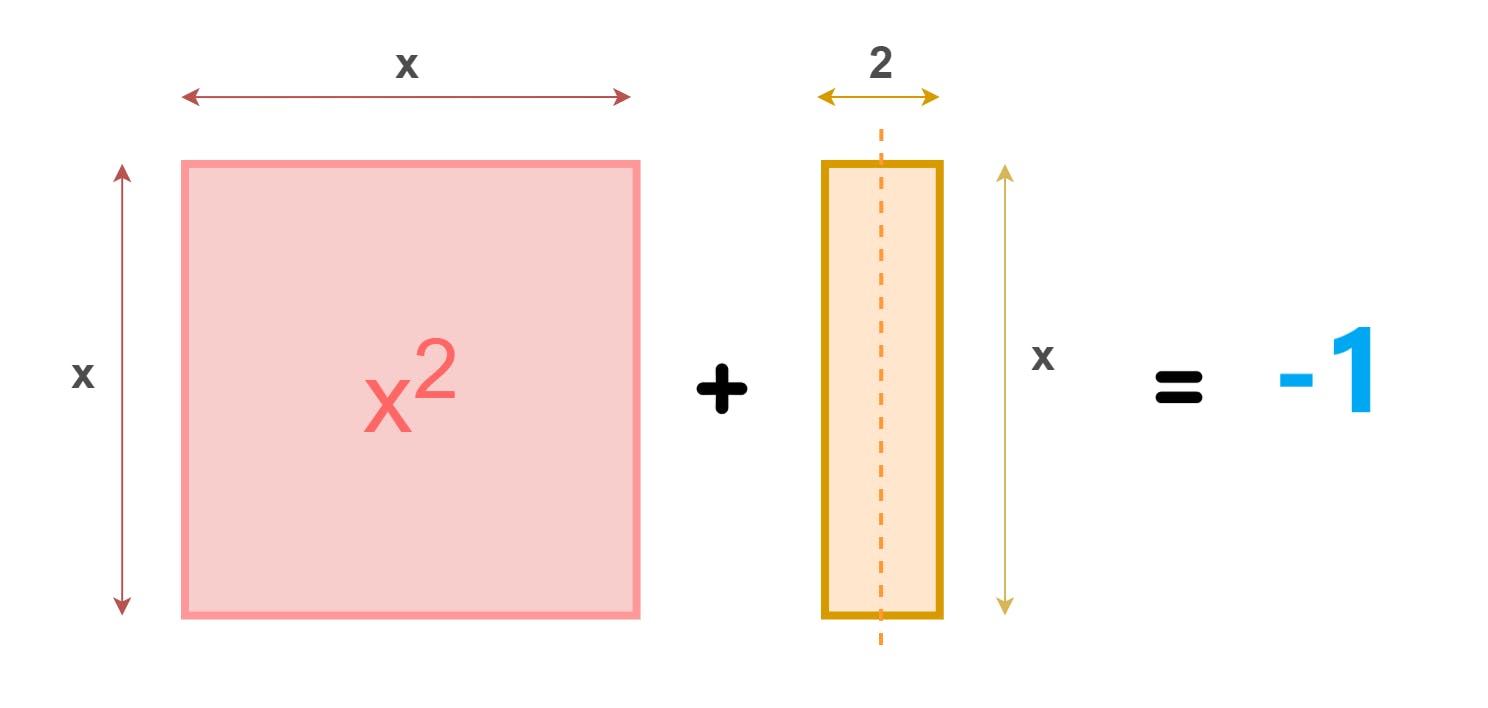
We can set aside -1 (constant) and concentrate only on the LHS. The LHS consists of

1. A square with area x² (length = x)
2. A rectangle with area 2x (length = x, breadth = 2)

The dashed line in the rectangle indicates that we can divide the rectangle into 2 halves. Now have

1. A Square with area x² (length = x)
2. 2 Rectangles with area x (length = x, breadth = 1) each.

Now, we rearrange our shapes to form a single square

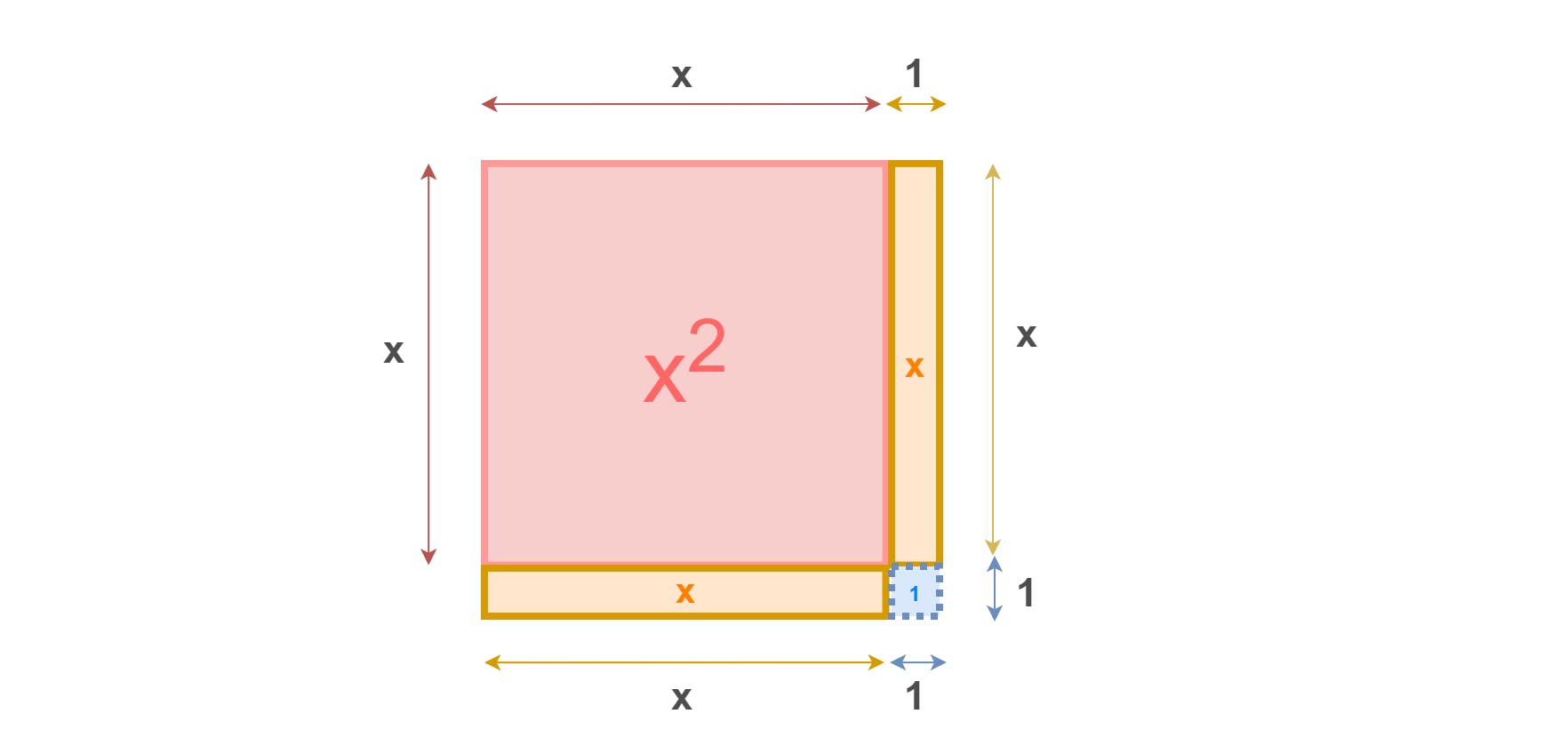
Along with our Square (x²) and two Rectangles (1x + 1x = 2x), we also get an unwanted square (1² = 1). So our equation becomes

x2 + 2x +1 = (x + 1)² according to a² + 2ab + b² = (a + b)²

To remove the unwanted square with area 1, we subract the above equation with 1 on either side

x² + 2x = (x + 1)² - 1

By substitute the above value in our actual equation x² + 2x = -1 we get

(x + 1)² - 1 = -1, by sending -1 to the RHS and taking square root we come up with

x = -1 which solves the equation x² + 2x = -1

This method can be very useful in Competitive Programming. You can solve Arranging Coins problem in LeetCode using this method. Arranging Coins - LeetCode You have a total of n coins that you want to form in a staircase shape, where every -th row must have exactly k coins…leetcode.com

Thank you 🤘

To know more about me, visit ganeshkumarm.me